What Is The Equation For Radius Of A Circle

Before deriving the equation of a circle, let us focus on what is a circle? A circle is a set of all points which are equally spaced from a fixed point in a plane. The fixed point is called the center of the circle.

The distance between the center and any point on the circumference is called the radius of the circle. Objects moving in circles have a speed which is equal to the distance traveled per time of travel. The distance around a circle is equivalent to a circumference and calculated as 2•pi•R where R is the radius. The time for one revolution around the circle is referred to as the period and denoted by the symbol T.

What Is The Formula For Radius Of A Circle Thus the average speed of an object in circular motion is given by the expression 2•pi•R / T. Often times the problem statement provides the rotational frequency in revolutions per minute or revolutions per second. Each revolution around the circle is equivalent to a circumference of distance. Thus, multiplying the rotational frequency by the circumference allows one to determine the average speed of the object. This will result in standard form, from which we can read the circle's center and radius.

Move the loose number over to the other side. Group the x-stuff and y-stuff together. Divide off by whatever is multiplied on the squared terms. Take the coefficient on the x-term, multiply by one-half, square, and add inside the x-stuff and also to the other side. Convert the left-hand side to squared form, and simplify the right-hand side.

If necessary, fiddle with signs and exponents to make your equation match the circle equation's format. The center is at ( 1/2, – 6/5 ) and the radius is 3/2. One difficulty a student may encounter in this problem set is the confusion as to which formula to use. The table below provides a useful summary of the formulas pertaining to circular motion and satellite motion. In the table, many of the formulas were derived from other equations. Thus, there will often be more than one means of determining an unknown quantity.

When you move around with respect to a specific point, then it forms a circle, only if you move in the fixed path. The point which you are taking as your references is called the centre of the circle. The path you follow while moving around forms the circumference of the circle. The distance that remains fixed while moving about a point is called the radius of a circle. Working with circles has always been very interesting. It is an important part of the mathematics concept to study.

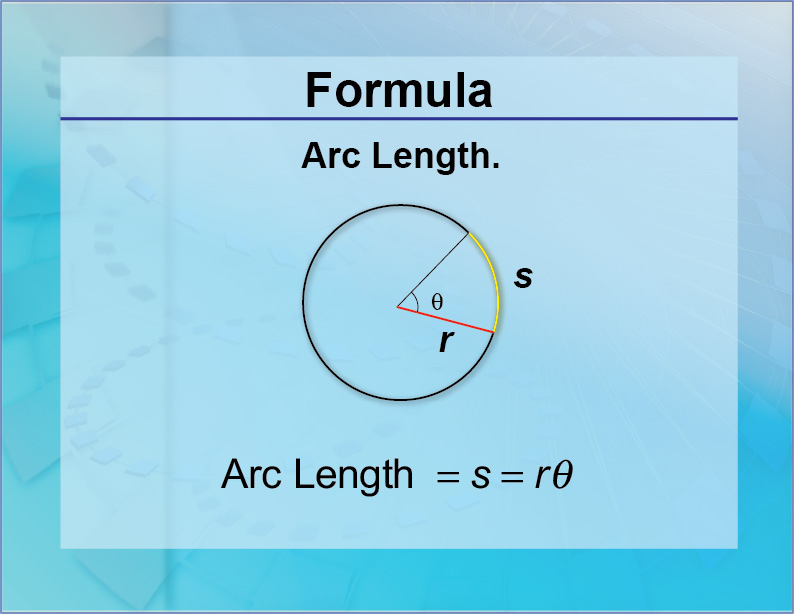
So let's change this equation so that it uses r[/latex] instead of c[/latex]. A circle is the set of points in a plane that are equidistant from a given point . The distance from the centeris called the radius, and the point is called the center. Twice the radius is known as the diameter . The angle a circle subtends from its center is a full angle, equal to or radians.

Sometimes in order to write the equation of a circle in standard form, you'll need to complete the square twice, once for x and once for y. Sometimes in order to write the equation of a circle in standard form, you'll need to complete the square twice, once for ??? In this lesson we'll look at how to write the equation of a circle in standard form in order to find the center and radius of the circle.

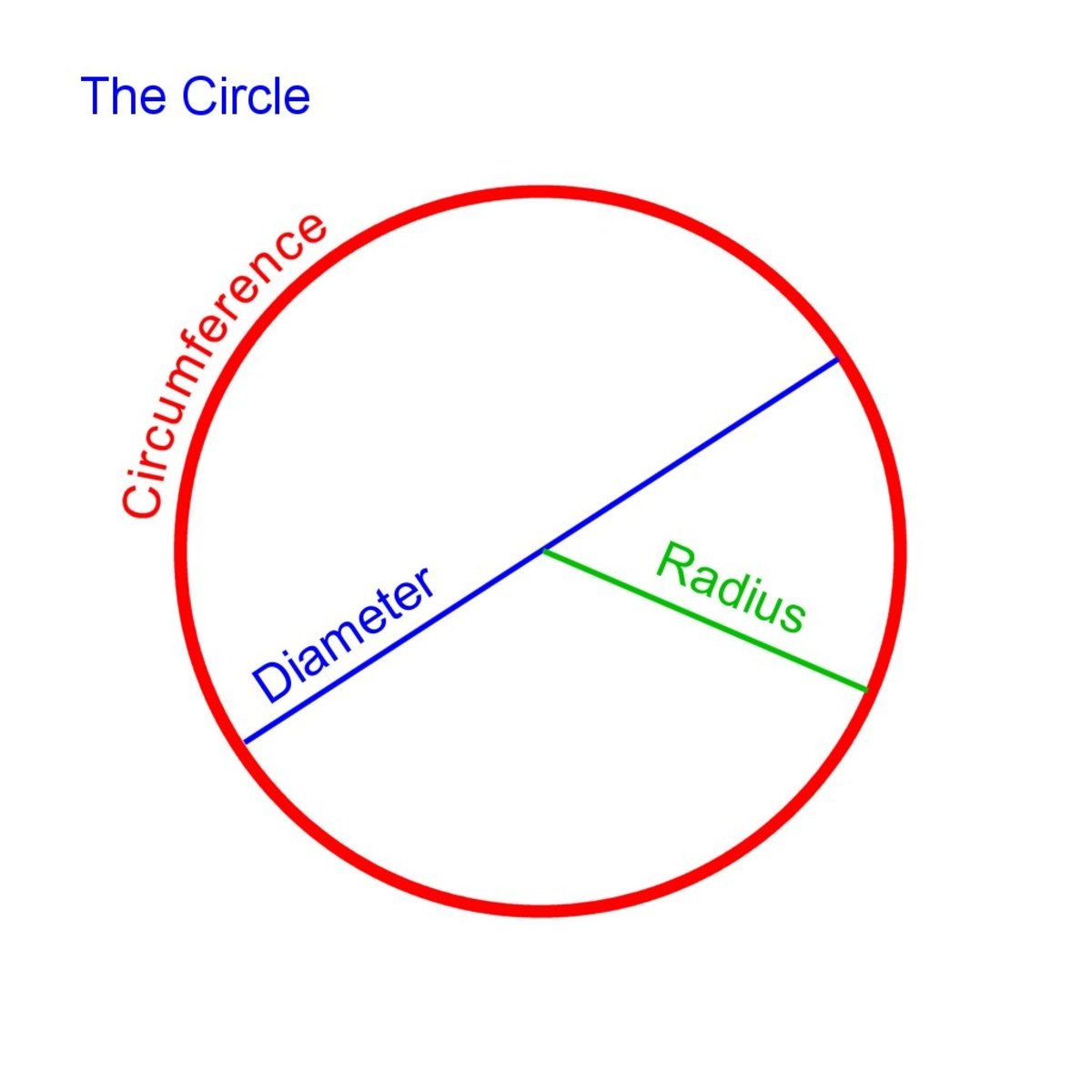
The radius, the diameter, and the circumference are the three defining aspects of every circle. Given the radius or diameter and pi you can calculate the circumference. The diameter is the distance from one side of the circle to the other at its widest points.

The diameter will always pass through the center of the circle. The radius is half of this distance. You can also think of the radius as the distance between the center of the circle and its edge. According to classical geometry, the radius of a circle is defined as the equal distance drawn from the centre to the circumference of the circle.

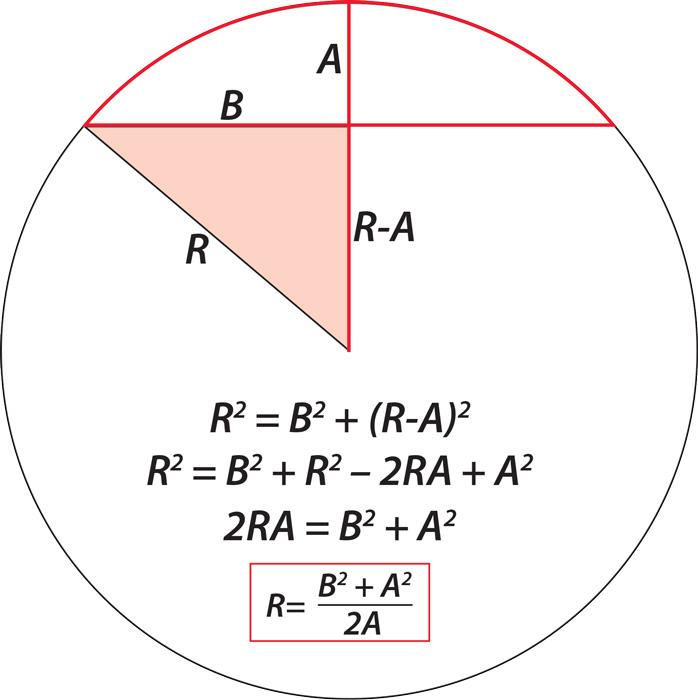
If we double this distance, then it becomes the diameter of the circle. This calculator can find the center and radius of a circle given its equation in standard or general form. Also, it can find equation of a circle given its center and radius.

The calculator will generate a step by step explanations and circle graph. The symbol pi is the ratio of the circumference of any circle to the diameter of that circle. If we were to look at the equation for circumference we can solve for pi. Two times the radius is also equal to the diameter.

Determine the center and radius given the equation of a circle in standard form. A circle represents a set of points, all of which are the same distance away from a fixed, middle point. This fixed point is called the center. The distance from the center of the circle to any point on the circle is called the radius.

An arc is a part of the circumference of the circle. It is part of a curve of a circle. A chord is the line segment drawn by the two different points on the circle. It is a straight line with both endpoints on the circle. The diameter is the longest chord of a circle that passes through the centre of the circle.

A sector is the portion of the circle formed by two radii of the circle and a sector helps in finding the length of the arc. In a circle, it is defined as a closed figure as other geometrical shapes and figures. However, the statement itself is contradictory. A circle has an inside and an outside area just like other geometric shapes.

However, it is contradictory in the fact that other shapes and figures like square, rectangle, triangle, and trapezium have some angles or straight sides. However, there are no such conditions in the case of the circle. It does not form any angle or the straight line. Thus the statement and definition of the circle are itself contradictory to the properties of a closed figure. Can be defined as a measure of distance from the centre of any circular object to its outermost edge or boundary. Problems range in difficulty from the very easy and straight-forward to the very difficult and complex.

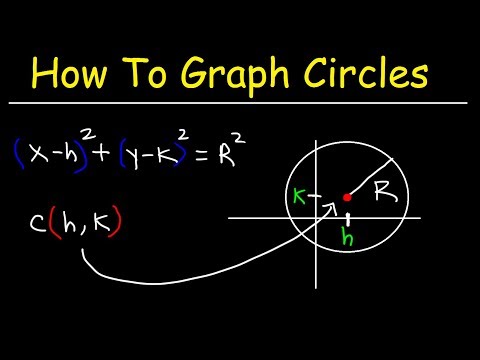
The more difficult problems are color-coded as blue problems. In most definitions of the conic sections, the circle is defined as a special case of the ellipse, when the plane is parallel to the base of the cone. However, it is also possible to begin with the definition of a circle and use graphical transformations to arrive at the general formula for an ellipse. This is the general formula for a circle with center \left(a,b\right)[/latex] and radius r[/latex]. Notice that all we have done is slightly rearrange the distance formula equation.

The inner line segments of the sector both equal the radius of the circle. The angle that these two measurements make is called a central angle. If an object does not have a center, the term may refer to its circumradius, the radius of its circumscribed circle or circumscribed sphere. In either case, the radius may be more than half the diameter, which is usually defined as the maximum distance between any two points of the figure. The inradius of a geometric figure is usually the radius of the largest circle or sphere contained in it.

The inner radius of a ring, tube or other hollow object is the radius of its cavity. Determine the standard form for the equation of the circle given its center and radius. Let us again imagine that a full pizza is divided into 8 equal sizes. Now let's rearrange the pieces in the form of a rectangle.

Now the base of the rectangle is the radius and the height is the half of circumference. Because both sides together make up the circle. So height becomes πr since circumference is 2πr. The circumference is the boundary enclosing the area within it. Term Definition Area Area is the space within the perimeter of a two-dimensional figure.

Circle A circle is the set of all points at a specific distance from a given point in two dimensions. Diameter Diameter is the measure of the distance across the center of a circle. The diameter is equal to twice the measure of the radius.

At this point we will be creating a perfect square trinomial for the x terms as well as the y terms. Recall that a perfect square trinomial is of the formand it factors in the form. When it is in that form it will allow us to continue onto the next step and write the equation in standard form,.

Divide the central angle into 360°. Multiply the resulting number by the arc length. That gives you the circumference of the circle. Half of the diameter is the radius of the circle. Now that you know how to calculate the circumference and area of a circle, you can use this knowledge to find the perimeter and area of composite figures. A Circle is defined as a closed figure as the other geometrical shapes and figures.

But, as we know, a Circle consists of an inside as well as an outside area like other geometric shapes. In a circle, however, there is no such property. It does not form any angle or a straight line. Where Mcentral is the mass of the central body about which the satellite orbits, R is the radius of orbit and G is 6.673 x N•m2/kg2. This ratio is only dependent upon the mass of the object which pulls the orbiting satellite inward.

This principle is consistent with as Kepler's third law of planetary motion. Movement along a circular path requires a net force directed towards the center of the circle. At every point along the path, the net force must be directed inwards.

Since net force and acceleration are always in the same direction, the acceleration of objects moving in circles must also be directed inward. In this equation, r[/latex] is the radius of the circle. A circle has only one radius—the distance from the center to any point is the same. To change our circle into an ellipse, we will have to stretch or squeeze the circle so that the distances are no longer the same.

First, let's start with a specific circle that's easy to work with, the circle centered at the origin with radius 1[/latex]. The radius is used to find many characteristics of a circle. If you wish to know the longest length across a circle, the diameter, you would multiply the radius by two. The circumference, or distance around the circle is found by multiplying two times the radius times pi.

The radius of a circle is a line drawn from the direct center of the circle to its outer edge. A radius can be drawn in any direction from the central point. A circle's radius is exactly half the length of the same circle's diameter, which is a line that divides the circle into two equal halves. In a spherical coordinate system, the radius describes the distance of a point from a fixed origin. The third coordinate may be called the height or altitude ,longitudinal position, or axial position. A circle is the set of points in a plane that lie a fixed distance from a given point, called the center.

This step isn't really part of finding the center or the radius. But in some cases you will need to graph your circle after finding those two items. You can graph your circle by plotting your center and then using your radius to find points on the circle.

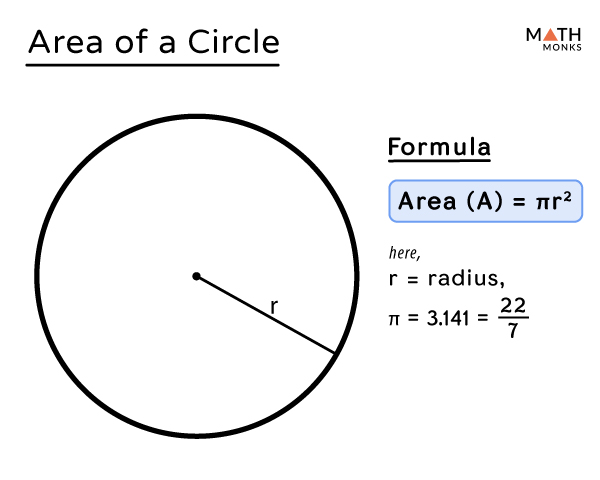
All points on the circle are a fixed distance away from the center . To find the equation of a circle given the radius and center of the circle, we can directly put the values in the standard form of the equation. This is the standard form of the equation. Thus, if we know the coordinates of the center of the circle and its radius as well, we can easily find its equation. The area of a circle is equal to pi times the radius squared.